CG #6

L'Expérience d'Eratosthène à la maison : prouvez que la Terre est ronde !

Eratosthène était un mathématicien, géographe, astronome et philosophe grec du IIIe siècle avant J.-C.

Né à Cyrène, une ancienne colonie grecque en Libye, il est surtout connu pour avoir été le premier à mesurer la circonférence de la Terre avec une précision remarquable.

En utilisant des méthodes géométriques et des observations astucieuses, il a pu démontrer que la Terre était ronde. En plus de ses contributions à la géographie, Eratosthène a également été le directeur de la célèbre bibliothèque d'Alexandrie, où il a mené de nombreuses recherches et écrit plusieurs ouvrages influents. Son travail a jeté les bases de nombreuses disciplines scientifiques et continue d'inspirer les chercheurs aujourd'hui.

L'expérience d'Eratosthène repose sur une observation simple mais brillante. Il avait remarqué qu'à midi, lors du solstice d'été, les rayons du soleil atteignaient le fond d'un puits à Syène (aujourd'hui Assouan, en Égypte), ce qui signifiait que le soleil était directement au-dessus. En revanche, à la même heure à Alexandrie, située à environ 800 kilomètres au nord de Syène, les objets projetaient une ombre. En mesurant l'angle de cette ombre, Eratosthène a pu déterminer l'angle de l'arc entre les deux villes.

En utilisant la distance entre Syène et Alexandrie et l'angle mesuré, Eratosthène a appliqué des principes géométriques pour calculer la circonférence de la Terre. Il a estimé cette distance à environ 5 000 stades (une unité de mesure grecque), et l'angle de l'ombre à environ 7,2 degrés, soit 1/50ème d'un cercle complet. En multipliant la distance par 50, il a obtenu une estimation de la circonférence de la Terre d'environ 250 000 stades, ce qui est remarquablement proche des mesures modernes.

Cette expérience a non seulement démontré que la Terre était ronde, mais elle a également fourni une méthode précise pour mesurer sa taille. Le travail d'Eratosthène a jeté les bases de la géographie et de l'astronomie modernes et continue d'inspirer les scientifiques et les passionnés de science à travers le monde.

"Pourquoi ne pas tenter cette expérience vous-même et prouver mathématiquement la sphéricité de la Terre depuis chez vous ?"

Dans le but de démontrer la sphéricité de la Terre, j'ai entrepris de vous présenter cette expérience en utilisant deux coordonnées familières. En mesurant les angles d'ombre à ces deux emplacements distincts, j'ai pu appliquer les principes géométriques d'Eratosthène.

De plus, j'ai développé un outil permettant de prédire les résultats de cette expérience. Cet outil utilise les données d'entrée pour effectuer des calculs basés sur :

• la date,
• les coordonnées terrestres, 
• la hauteur d'un référentiel.

Il prend en compte :

• l'altitude apparente du Soleil, 
• l'équation du temps, 
• le midi solaire à chaque point, 
• la longueur anticipée des ombres,
• le rayon de la Terre, 

Il offre ainsi une méthode pratique et précise pour vérifier la rondeur de notre planète depuis chez soi. 

Cette étude est organisée en 4 grandes parties :

• l'Expérience,
• La Théorie,
• L'Outil de calcul,
• L'Application.

L'Expérience

• Base géométrique

Dans le cas d'une expérience à l'équateur comme a pu le faire Eratosthène au IIIe siècle av. J.-C., le calcul est simplifié. Dans notre cas, car aucun ne se situe à l'équateur, l'algorithme est plus complexe.

• Étape 1 : Déterminer les angles α1 et α2 grâce aux hauteurs des référentiels h1 et h2 et aux longueurs des ombres l1 et l2. L'angle devra être exprimé en radian :

• Étape 2 : En calculant les angles α1 et α2, on détermine l'angle α3 par soustraction.

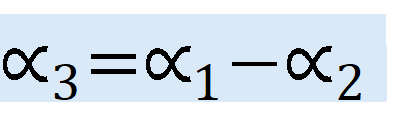
• Étape 3 : Par la loi des sinus et grâce à l'angle α3 et à la distance d entre les deux sites, on détermine la longueur des deux côtés du triangle isocèle. L'angle devra être exprimé en radian :

• Complément : · Il est également possible de calculer R par un produit en croix afin de déterminer le périmètre.

La Théorie

• Calcul du jour Julien

Le jour julien est un système de datation utilisé principalement en astronomie pour simplifier les calculs liés aux dates. Il s'agit d'une manière continue de compter les jours à partir d'une époque de référence, qui est le 1er janvier 4713 avant J.-C. à midi (en temps universel). Chaque jour julien est un nombre entier, et les fractions de jour sont exprimées sous forme décimale, ce qui permet de représenter des moments précis dans la journée.

Pourquoi utiliser le jour julien en astronomie ?

• Simplicité des calculs :

Contrairement au calendrier grégorien ou julien, qui ont des mois de durées différentes et des années bissextiles, le jour julien est une échelle de temps linéaire. Cela élimine les complications dues aux variations du calendrier, facilitant ainsi les calculs temporels, comme la différence entre deux dates ou la prévision des positions des objets célestes. 

• Précision :

Le jour julien permet une précision extrêmement fine dans le temps. Puisque les fractions de jour peuvent être exprimées sous forme décimale, il est possible de définir un instant précis jusqu'à la seconde ou même à des échelles de temps encore plus petites, ce qui est crucial dans les observations astronomiques de phénomènes rapides ou pour synchroniser les événements entre différents observatoires. 

• Universalité :

Le jour julien est utilisé de manière uniforme par les astronomes du monde entier, quelle que soit la culture ou le système de calendrier utilisé localement. Cette standardisation est essentielle pour la collaboration internationale et pour la comparaison de données recueillies à différentes époques et dans différents lieux.

En résumé, le jour julien est un outil indispensable en astronomie pour la simplicité, la précision et l'universalité qu'il apporte aux calculs de temps et à la datation des événements célestes.

• Calcul des coordonnées Terrestres

Le calcul des coordonnées terrestres se décompose en plusieurs étapes essentielles :

• Conversion des coordonnées en écriture décimale :

Les coordonnées géographiques, exprimées en degrés, minutes et secondes, doivent être converties en décimales. Rappelons que 1° équivaut à 60 minutes d'arc (60') ou 3600 secondes d'arc (3600"). Pour effectuer la conversion, on additionne les minutes divisées par 60 et les secondes divisées par 3600 au degré correspondant. Par exemple, 45° 30' 0" devient 45 + 30/60 = 45,5°.

• Interprétation des coordonnées

En matière de longitude, les valeurs à l'est du méridien de Greenwich sont positives, tandis que celles à l'ouest sont négatives (de -90 à +90°). Pour la latitude, les valeurs dans l'hémisphère nord sont positives, tandis que celles dans l'hémisphère sud sont négatives (de -180 à +180°C).

• Conversion du temps et des angles

La Terre effectue une rotation complète de 360° en 24 heures, ce qui signifie qu'elle tourne de 15° par heure. Cela correspond à un décalage de 1° toutes les 4 minutes. Ce décalage est important pour le calcul du temps de latence associé à un changement de longitude. Le temps de latence (Δt) peut donc être calculé comme suit (pour un résultat en minutes) :

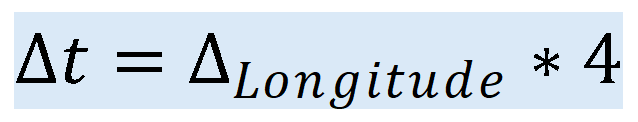
Ainsi, chaque degré de différence en longitude se traduit par un décalage de 4 minutes dans le temps.

• Calcul des distances en latitude et longitude

Une fois les coordonnées converties, la distance entre deux points sur le globe peut être estimée en utilisant les différences de latitude et de longitude. En latitude, chaque degré correspond à environ 110,95 km, basé sur un périmètre terrestre de 39 941 km. En longitude, la distance par degré dépend de la latitude et est de 111,32 km à l'équateur (avec un périmètre de 40 075 km), mais elle diminue en direction des pôles. La distance en longitude pour une latitude donnée est ajustée par le cosinus de cette latitude.

Il est important de noter que la Terre n'est pas une sphère parfaite, mais un géoïde, légèrement aplati aux pôles et bombé à l'équateur. Cette forme irrégulière influence les calculs de distance, rendant les conversions en latitude et longitude approximatives, surtout sur de longues distances.

• Estimation de la distance totale :

Enfin, pour obtenir la distance totale entre deux points, on peut utiliser la formule haversine, utilisée pour calculer la distance entre deux points sur une sphère en tenant compte de la courbure de la Terre.

Où (R) est le rayon de la Terre (environ 6 371 km), (a) est une variable intermédiaire, et (d) est la distance entre les deux points. Φ représente les latitudes de chaque point et λ les longitudes de chaque point. 

• Calcul des coordonnées du Soleil

Les coordonnées du Soleil sont essentielles pour comprendre sa position dans le ciel à un moment donné, en tenant compte de divers paramètres astronomiques.

• Temps (T) :

Il représente le temps écoulé depuis une époque de référence. Ce temps est utilisé pour calculer la position actuelle du Soleil sur son orbite. Il est mesuré en siècles juliens de 36525 jours des éphémérides à partir du 0,5 janvier 1990 TE.

• Longitude moyenne du Soleil (L) :

Il s'agit de la position angulaire moyenne du Soleil par rapport à un point de référence sur l'écliptique. Elle augmente régulièrement avec le temps, reflétant le mouvement du Soleil sur son orbite.

• Anomalie moyenne du Soleil (M) :

C'est l'angle qui mesure la position moyenne du Soleil sur une orbite circulaire fictive. Elle aide à estimer la véritable position du Soleil malgré l'orbite elliptique de la Terre.

• Excentricité de l'orbite terrestre (e) :

L'excentricité décrit l'étirement de l'orbite terrestre. Une orbite parfaitement circulaire aurait une excentricité de 0, tandis que celle de la Terre est légèrement elliptique, avec une excentricité d'environ 0,0167.

• Longitude vraie du Soleil (ϴ) :

Elle est obtenue en ajoutant l'équation du centre (C) à la longitude moyenne (L), donnant ainsi la position angulaire réelle du Soleil sur l'écliptique.

• Anomalie vraie du Soleil (υ)

C'est l'angle réel entre le Soleil, la Terre et le point de l'orbite le plus proche du Soleil. Elle donne une mesure précise de la position du Soleil sur son orbite.

• Rayon vecteur du Soleil (R)

C'est la distance entre la Terre et le Soleil à un instant donné, qui varie légèrement en raison de l'excentricité de l'orbite terrestre.

• Variable (Ω)

Elle peut désigner divers éléments selon le contexte, mais souvent elle représente la longitude du nœud ascendant, le point où le Soleil traverse l'écliptique vers le nord.

• Longitude apparente du Soleil (ϴ_app)

Cette valeur ajuste la longitude vraie du Soleil pour prendre en compte des effets comme l'aberration de la lumière et la nutation de la Terre. Elle représente la position observée du Soleil dans le ciel.

• Obliquité de l'Ecliptique (ε)

C'est l'angle entre le plan de l'écliptique et l'équateur céleste. Actuellement d'environ 23,4°, cette inclinaison est responsable des saisons.

• Position apparente du Soleil (ε)

C'est la position du Soleil sur la sphère céleste, influencée par l'obliquité de l'écliptique.

• Déclinaison du Soleil (δ)

Il s'agit de l'angle entre le Soleil et l'équateur céleste, variant au cours de l'année entre +23,4° et -23,4°, déterminant la hauteur du Soleil dans le ciel à midi.

• Altitude du Soleil au point n°1 et n°2 (h1, h2)

Ces altitudes mesurent la hauteur du Soleil au-dessus de l'horizon à deux points spécifiques, souvent utilisés pour déterminer les moments du lever et du coucher du Soleil.

Ces concepts permettent de calculer et de prédire avec précision la position du Soleil dans le ciel, ce qui est essentiel pour l'astronomie, la navigation et même l'organisation des calendriers.

• Calcul de l'équation du temps

L'équation du temps est la différence entre le temps solaire vrai et le temps solaire moyen. Cette différence varie tout au long de l'année en raison de deux principaux facteurs :

• L'orbite elliptique de la Terre

La Terre ne tourne pas autour du Soleil en cercle parfait, mais en ellipse. Cela signifie que la vitesse de la Terre varie au cours de l'année.

• Inclinaison de l'axe de rotation de la Terre

L'axe de rotation de la Terre est incliné par rapport à son plan orbital, ce qui affecte la position apparente du Soleil dans le ciel.

En conséquence, le midi solaire (le moment où le Soleil est au plus haut dans le ciel) ne coïncide pas toujours avec le midi moyen (12h00 sur nos horloges). L'équation du temps peut atteindre jusqu'à ±16 minutes. Elle est positive lorsque le temps solaire vrai est en avance sur le temps solaire moyen et négative dans le cas contraire.

Elle est la différence entre le temps solaire apparent (le temps basé sur la position réelle du Soleil dans le ciel) et le temps solaire moyen (le temps basé sur une hypothétique orbite circulaire et non inclinée de la Terre).

Ce phénomène est crucial pour les astronomes et les horlogers, car il permet de corriger les horloges solaires et de comprendre les variations saisonnières de la durée du jour.

Tous les calculs précédents liés aux coordonnées de la Terre et du Soleil sont essentiels pour déterminer avec précision l'équation du temps.

• Evolution du temps sur une année complète

L'évolution de l'équation du temps sur une année complète est représentée par la courbe rouge sur la figure ci-contre. 

En première approximation, sa forme s'analyse comme résultant de la superposition de deux sinusoïdes :

En bleu sur le diagramme : Une sinusoïde de période égale à un an, d'amplitude égale à 7,66 minutes et s'annulant aux passages de la Terre aux apsides : périgée le 3 janvier et apogée début juillet. Cette composante reflète l'excentricité de l'orbite terrestre.

En vert sur le diagramme : Une sinusoïde de période égale à une demi-année, d'amplitude 9,87 minutes et s'annulant aux solstices et aux équinoxes. Cette composante résulte de l'obliquité de l'écliptique sur l'équateur.

L'équation du temps, en rouge, s'annule quatre fois par an, vers le 15 avril, le 13 juin, le 1er septembre et le 25 décembre. Son maximum, atteint vers le 11 février, vaut 14 min 15 s, et son minimum, atteint vers le 3 novembre, vaut − 16 min 25 s.

L'évolution annuelle de l'équation du temps, en un lieu donné, peut être visualisée à l'aide d'une courbe appelée analemme ou courbe en 8.

L'analemme est une figure en forme de huit que l'on obtient en traçant la position du Soleil dans le ciel à la même heure chaque jour pendant une année. Cette figure est le résultat de deux phénomènes principaux : l'excentricité de l'orbite terrestre et l'inclinaison de l'axe de rotation de la Terre.

Excentricité de l'orbite terrestre :

La Terre ne tourne pas autour du Soleil en cercle parfait, mais en ellipse. Cela signifie que la vitesse de la Terre varie au cours de l'année, ce qui affecte la position apparente du Soleil dans le ciel.

Inclinaison de l'axe de rotation de la Terre :

L'axe de rotation de la Terre est incliné par rapport à son plan orbital. Cette inclinaison provoque des variations saisonnières dans la hauteur du Soleil dans le ciel à une heure donnée.

L'analemme est souvent représenté sur les globes terrestres et les cadrans solaires pour montrer la variation de la position du Soleil au cours de l'année. La forme en huit de l'analemme est due à la combinaison des effets de l'excentricité de l'orbite terrestre et de l'inclinaison de l'axe terrestre. En observant l'analemme, on peut comprendre comment ces deux facteurs influencent la durée du jour et la hauteur du Soleil dans le ciel.

• Calcul du midi solaire

Le midi solaire, ou midi vrai, est le moment où le Soleil atteint son point le plus haut dans le ciel pour un lieu donné.

Contrairement à ce que l'on pourrait penser, ce moment ne coïncide pas toujours avec 12h00 sur nos horloges. La position du Soleil à midi dépend de plusieurs facteurs, notamment la longitude exacte du lieu, la date et le fuseau horaire. En France, le fuseau horaire est UTC+1 en hiver et UTC+2 en été.

Pour déterminer l'heure exacte du midi solaire, il est nécessaire de prendre en compte ces éléments ainsi que l'équation du temps, qui corrige les petites différences causées par l'orbite elliptique de la Terre et l'inclinaison de son axe. La formule pour calculer l'heure du midi solaire est la suivante :

Avec : T_midi : Temps du midi solaire ; L_référence : Longitude de référence (en général celui du méridien central du fuseau horaire) ; L_locale : Longitude locale ; Et_t : Équation du temps

• Calcul du rayon de la Terre (par anticipation à l'expérience)

Pour calculer le rayon de la Terre, nous pouvons nous inspirer de l'expérience d'Eratosthène. Cette méthode repose sur l'observation des ombres projetées par des objets verticaux à deux endroits différents situés sur le même méridien. Voici comment procéder :

• Détermination des altitudes du Soleil

En utilisant les calculs des coordonnées terrestres et solaires, ainsi que l'équation du temps, nous pouvons déterminer avec précision les altitudes du Soleil à chaque point d'observation. Ces altitudes sont essentielles pour calculer les longueurs des ombres.

• Calcul des longueurs des ombres

À l'aide de la trigonométrie, et en connaissant les altitudes du Soleil, il est possible de calculer les longueurs des ombres projetées par des objets verticaux. Cela nécessite un référentiel déterminé pour assurer la précision des mesures.

• Soustraction des angles solaires

En mesurant les angles ou altitudes du Soleil à deux points différents et en soustrayant ces valeurs, nous obtenons l'angle entre les deux points d'observation par rapport au centre de la Terre.

• Calcul de la distance en latitude

La distance en latitude entre les deux points d'observation doit être connue. Cette distance, combinée avec l'angle obtenu précédemment, permet de déterminer le rayon de la Terre.

En reprenant les calculs précédemment énumérés, nous pouvons ainsi déterminer le rayon de la Terre avec une grande précision, tout comme l'avait fait Eratosthène il y a plus de deux mille ans.

Un outil de calcul Excel sera réalisé pour plus de commodité et d'efficacité dans les calculs.

L'outil de calcul

Pour plus de commodité et d'efficacité dans la réalisation des expériences, un outil Excel a été réalisé.

• Calcul du rayon Terrestre

• Validation de l'expérience originale

Cet outil permet notamment de refaire l'expérience d'Eratosthène à x date. La valeur de l'angle déterminée est de 7,13° contre 7,20° mesure par Eratosthène.

La date n'est pas évidemment renseignée correctement, ci-dessus au 30 septembre 2024.

• Contrôle des données de l'outil

Hypothèse 1 : Date : 1er juin 2024 ; Hypothèse 2 : Coordonnées GPS : 3°07'50''W (première capture d'écran de l'outil). (la latitude est masquée pour des raison de confidentialité)

Exemple 1 : les calculs de l'équation du temps se vérifient avec une marge d'erreur de ±5sec ; ce qui est convenable pour cette expérience.

Exemple 2 : les calculs du midi solaire ou soleil au zénith se vérifient avec une marge d'erreur de ±3 min ; ce qui est convenable pour cette expérience. L'ordre de grandeur est correct.

Exemple 3 : les calculs de l'altitude du Soleil au-dessus de l'horizon se vérifient avec une marge d'erreur quasiment nulle (résultat identique : 64°,18) :

Exemple 5 : Nous retrouvons les valeurs mesurées par Eratosthène avec un angle de 7,13° contre 7,2° sachant qu'il n'avait pas les outils de mesure adaptés à l'époque.

L'Application

• Hypothèse de l'expérience

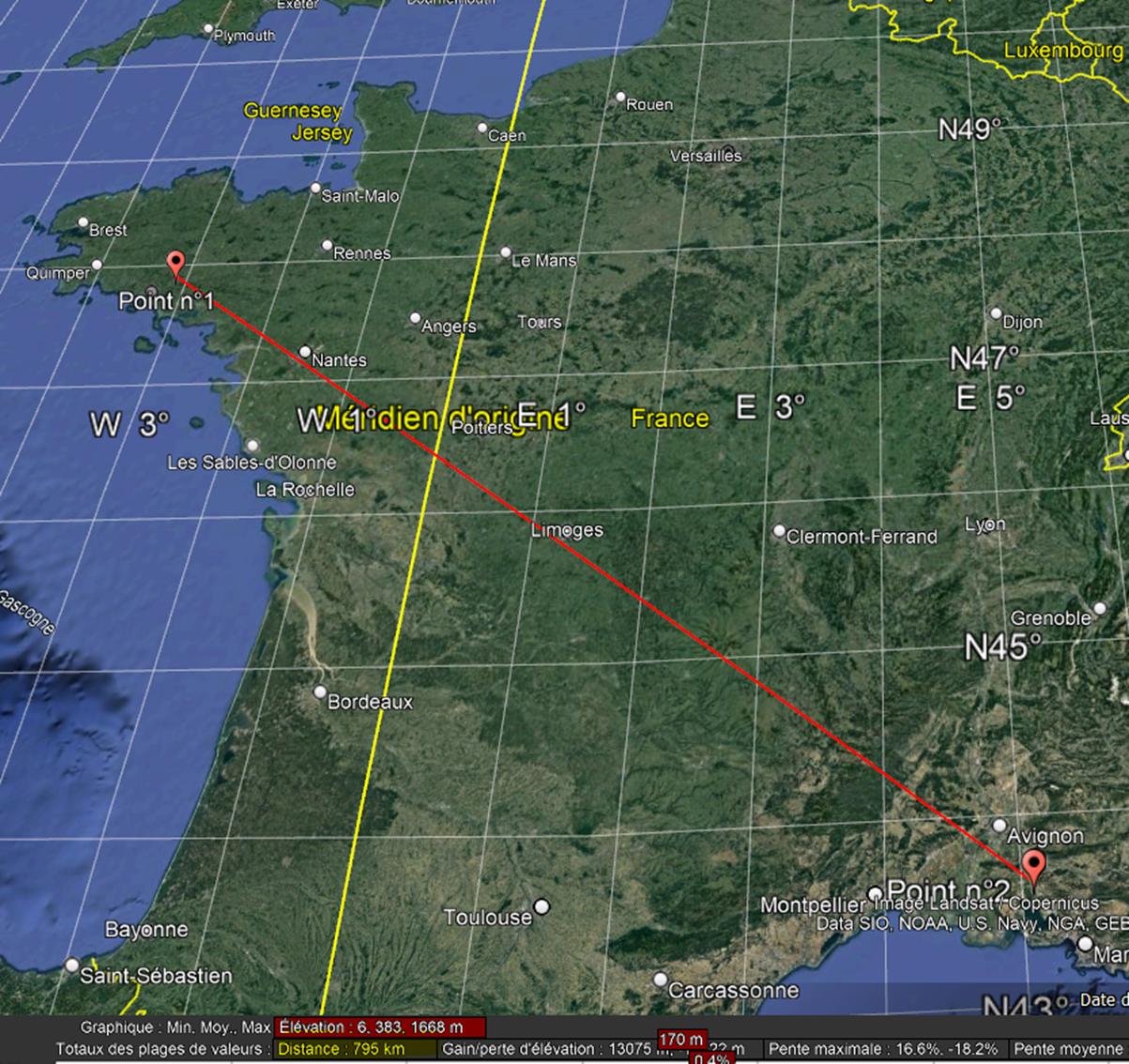
• La première mesure sera effectuée en Provence-Alpes-Côte d'Azur (Point n°2) : Coordonnées : 5°05'14''W. (la latitude est masquée pour des raison de confidentialité) 
• La deuxième mesure sera effectuée en Bretagne (Point n°1) : Coordonnées : 3°07'50''W. (la latitude est masquée pour des raison de confidentialité)

• Les deux mesures seront effectuées le 30 septembre 2024.
• Les deux mesures étant effectuées à des longitudes différentes, un ajustement temporel de l'expérience sera nécessaire. De plus, une correction liée à l'équation du temps devra être appliquée pour s'assurer que les mesures soient prises au moment précis du midi solaire. Midis solaires calculés : Point n°1 en Bretagne : 14h02 ; Point n°2 en Provence-Alpes-Côte d'Azur : 13h30
• Le référentiel sera un poteau à la perpendiculaire du sol et fixé sur une règle graduée elle-même à niveau et maintenu par deux supports au sol. 
• Ce référencie aura une hauteur de 1,000 m et la règle, une hauteur de 1,500 m.
• La hauteur « h » du référentiel devra être parfaitement mesuré.
• L'ombre du référentiel devra être relevé sur une règle graduée parfaitement à niveau et maintenu par deux supports.

Le résultat obtenu est une longueur d'ombre de 1,23 m pour le premier point et 1,06 m pour le deuxième point.

• Mesure et résultat de l'expérience

• L'ombre au premier point à l'Est (point n°2) a une longueur de : l_2 = 
• L'ombre au premier point à l'Ouest (point n°1) a une longueur de : l_1 = 

Par le calcul trigonométrique, nous trouvons :

• Un angle au premier point à l'Est (point n°2) a une longueur de : α_2 = 
• Un angle au premier point à l'Ouest (point n°1) a une longueur de : α_1 = 
• L'angle permettant le calcul par la loi des sinus est donc de : α_3 = α_1 - α_2 = 
• D'après la loi des sinus, le rayon de la Terre calculé est de : A remplir

Les résultats expérimentaux confirment les prédictions théoriques. Le rayon terrestre mesuré et calculé est en accord étroit avec les modèles existants. Dans les deux cas, la preuve de la sphéricité de la Terre est indiscutable.

Je vous propose ici un outil développé en C# .NET fonctionnant avec la console Windows.

Il s'agit d'une calculatrice anticipative de l'Expérience d'Eratosthène qui permet de calculer grâce à la date et de deux points GPS :

• les coordonnées solaires (dont l'altitude apparente du Soleil)
• l'équation du temps
• le midi solaire à chaque point avec le delta
• la taille de l'ombre d'un référentiel que dont tu sélectionneras la hauteur
• le rayon calculé de la Terre

Il va prédire l'expérience.